Jika anda menggunakan HP maka gunakan mode LANDSCAPE agar equation tidak terpotong
LANGKAH-LANGKAH MENGGUNAKAN TEKNIK SUBSTITUSI PADA INTEGRAL FUNGSI ALJABAR SECARA UMUM
- Fungsi yang mengandung pangkat tertinggi kita misalkan dengan $u$. Apabila kedua fungsi pangkatnya sama maka fungsi yang lebih kompleks kita misalkan sebagai $u$.
- Turunkan $u$ terhadap $x$ dan kita dapatkan hasilnya (misal $a$) kemudian ubah ke bentuk $dx$. $\displaystyle\frac{d u}{d x}=a \rightarrow d x=\frac{d u}{a}$.
- Substitusikan $u$ dan $dx$ ke soal kemudian diintegralkan.
- Ubah kembali fungsi $u$ menjadi fungsi awal.
Integral substitusi dapat juga dirumuskan sebagai berikut:
Contoh Soal
Soal 1
Pembahasan:
${\text{misalkan }}u = 3{x^2} + 5,{\text{ maka }}\frac{{du}}{{dx}} = 6x{\text{ atau }}dx = \frac{{du}}{{6x}}, {\text{ sehingga: }}$
$\begin{align} &\int {x{{\left( {3{x^2} + 5} \right)}^4}\;dx} \hfill \\ &= \int {x \cdot {u^4}\;\frac{{du}}{{6x}}} \hfill \\ &= \frac{1}{6}\int {{u^4}\;du} \hfill \\ &= \frac{1}{6} \cdot \frac{{{u^5}}}{5} + c \hfill \\ &= \boxed{\frac{1}{{30}}{\left( {3{x^2} + 5} \right)^5} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &\int {x{{\left( {3{x^2} + 5} \right)}^4}\;dx} \hfill \\ &= \int {\frac{{x{{\left( {3{x^2} + 5} \right)}^4}}}{{6x}}} \;d({3{x^2} + 5}) \hfill \\ &= \frac{1}{{6 \cdot 5}}{\left( {3{x^2} + 5} \right)^5} + c \hfill \\ &= \boxed{\frac{1}{{30}}{{\left( {3{x^2} + 5} \right)}^5} + c} \hfill \\ \end{align} $
${\text{misalkan }}u = 3{x^2} + 5,{\text{ maka }}\frac{{du}}{{dx}} = 6x{\text{ atau }}dx = \frac{{du}}{{6x}}, {\text{ sehingga: }}$
$\begin{align} &\int {x{{\left( {3{x^2} + 5} \right)}^4}\;dx} \hfill \\ &= \int {x \cdot {u^4}\;\frac{{du}}{{6x}}} \hfill \\ &= \frac{1}{6}\int {{u^4}\;du} \hfill \\ &= \frac{1}{6} \cdot \frac{{{u^5}}}{5} + c \hfill \\ &= \boxed{\frac{1}{{30}}{\left( {3{x^2} + 5} \right)^5} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &\int {x{{\left( {3{x^2} + 5} \right)}^4}\;dx} \hfill \\ &= \int {\frac{{x{{\left( {3{x^2} + 5} \right)}^4}}}{{6x}}} \;d({3{x^2} + 5}) \hfill \\ &= \frac{1}{{6 \cdot 5}}{\left( {3{x^2} + 5} \right)^5} + c \hfill \\ &= \boxed{\frac{1}{{30}}{{\left( {3{x^2} + 5} \right)}^5} + c} \hfill \\ \end{align} $
Soal 2
Pembahasan:
$\begin{align} &u = {x^2} + 3x \hfill \\ &\frac{{du}}{{dx}} = 2x + 3 \to dx = \frac{{du}}{{2x + 3}} \hfill \\ \end{align}$
$\begin{align} &\int {{u^4}\left( {2x + 3} \right)} \frac{{du}}{{2x + 3}} \hfill \\ &= \frac{1}{5}{u^5} + c \hfill \\ &= \boxed{\frac{1}{5}{\left( {{x^2} + 3x} \right)^5} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &= \int {\frac{{{{\left( {{x^2} + 3x} \right)}^4}}}{{\left( {2x + 3} \right)}}\left( {2x + 3} \right)\;d({x^2} + 3x}) \hfill \\ &= \boxed{\frac{1}{5}{{\left( {{x^2} + 3x} \right)}^5} + c} \hfill \\ \end{align} $
$\begin{align} &u = {x^2} + 3x \hfill \\ &\frac{{du}}{{dx}} = 2x + 3 \to dx = \frac{{du}}{{2x + 3}} \hfill \\ \end{align}$
$\begin{align} &\int {{u^4}\left( {2x + 3} \right)} \frac{{du}}{{2x + 3}} \hfill \\ &= \frac{1}{5}{u^5} + c \hfill \\ &= \boxed{\frac{1}{5}{\left( {{x^2} + 3x} \right)^5} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &= \int {\frac{{{{\left( {{x^2} + 3x} \right)}^4}}}{{\left( {2x + 3} \right)}}\left( {2x + 3} \right)\;d({x^2} + 3x}) \hfill \\ &= \boxed{\frac{1}{5}{{\left( {{x^2} + 3x} \right)}^5} + c} \hfill \\ \end{align} $
Soal 3
Pembahasan:
$\begin{align} &u = {x^3} - {x^2} - 1 \hfill \\ &\frac{{du}}{{dx}} = 3{x^2} - 2x \to dx = \frac{{du}}{{3{x^2} - 2x}} \hfill \\ \end{align}$
$\begin{align} &u = {x^3} - {x^2} - 1 \hfill \\ &\frac{{du}}{{dx}} = 3{x^2} - 2x \to dx = \frac{{du}}{{3{x^2} - 2x}} \hfill \\ &= \int {\left( {4x - 6{x^2}} \right)} \sqrt u \frac{{du}}{{3{x^2} - 6x}} \hfill \\ &= \int { - 2\left( {3{x^2} - 2x} \right){u^{\frac{1}{2}}}} \frac{{du}}{{3{x^2} - 2x}} \hfill \\ &= - 2\int {{u^{\frac{1}{2}}}\;du} \hfill \\ &= \frac{{ - 2}}{{\frac{3}{2}}}{u^{\frac{3}{2}}} + c \hfill \\ &= - \frac{4}{3}u\sqrt u + c \hfill \\ &= \boxed{ - \frac{4}{3}\left( {{x^3} - {x^2} - 1} \right)\sqrt {{x^3} - {x^2} - 1} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &\int {\left( {4x - 6{x^2}} \right)\frac{{{{\left( {{x^3} - {x^2} - 1} \right)}^{\frac{1}{2}}}}}{{\left( {3{x^2} - 2x} \right)}}} \;d\left( {{x^3} - {x^2} - 1} \right) \hfill \\ &= - 2\int {{{\left( {{x^3} - {x^2} - 1} \right)}^{\frac{1}{2}}}} \;d\left( {{x^3} - {x^2} - 1} \right) \hfill \\ &= - 2 \cdot \frac{2}{3}{\left( {{x^3} - {x^2} - 1} \right)^{\frac{3}{2}}} + c \hfill \\ &= \boxed{ - \frac{4}{3}\left( {{x^3} - {x^2} - 1} \right)\sqrt {{x^3} - {x^2} - 1} + c} \hfill \\ \end{align} $
$\begin{align} &u = {x^3} - {x^2} - 1 \hfill \\ &\frac{{du}}{{dx}} = 3{x^2} - 2x \to dx = \frac{{du}}{{3{x^2} - 2x}} \hfill \\ \end{align}$
$\begin{align} &u = {x^3} - {x^2} - 1 \hfill \\ &\frac{{du}}{{dx}} = 3{x^2} - 2x \to dx = \frac{{du}}{{3{x^2} - 2x}} \hfill \\ &= \int {\left( {4x - 6{x^2}} \right)} \sqrt u \frac{{du}}{{3{x^2} - 6x}} \hfill \\ &= \int { - 2\left( {3{x^2} - 2x} \right){u^{\frac{1}{2}}}} \frac{{du}}{{3{x^2} - 2x}} \hfill \\ &= - 2\int {{u^{\frac{1}{2}}}\;du} \hfill \\ &= \frac{{ - 2}}{{\frac{3}{2}}}{u^{\frac{3}{2}}} + c \hfill \\ &= - \frac{4}{3}u\sqrt u + c \hfill \\ &= \boxed{ - \frac{4}{3}\left( {{x^3} - {x^2} - 1} \right)\sqrt {{x^3} - {x^2} - 1} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &\int {\left( {4x - 6{x^2}} \right)\frac{{{{\left( {{x^3} - {x^2} - 1} \right)}^{\frac{1}{2}}}}}{{\left( {3{x^2} - 2x} \right)}}} \;d\left( {{x^3} - {x^2} - 1} \right) \hfill \\ &= - 2\int {{{\left( {{x^3} - {x^2} - 1} \right)}^{\frac{1}{2}}}} \;d\left( {{x^3} - {x^2} - 1} \right) \hfill \\ &= - 2 \cdot \frac{2}{3}{\left( {{x^3} - {x^2} - 1} \right)^{\frac{3}{2}}} + c \hfill \\ &= \boxed{ - \frac{4}{3}\left( {{x^3} - {x^2} - 1} \right)\sqrt {{x^3} - {x^2} - 1} + c} \hfill \\ \end{align} $
Soal 4
Pembahasan:
$\begin{align} &u = {x^4} - 1 \hfill \\ &\frac{{du}}{{dx}} = 4{x^3} \to dx = \frac{{du}}{{4{x^3}}} \hfill \\ \end{align}$
$\begin{align} &= \int {\frac{{{x^3}}}{{{u^{20}}}}} \frac{{du}}{{4{x^3}}} \hfill \\ &= \frac{1}{4}\int {{u^{ - 20}}\; + c} \hfill \\ &= \frac{1}{4} \cdot \frac{1}{{\left( { - 19} \right)}}{u^{ - 19}} + c \hfill \\ &= \boxed{ - \frac{1}{{76{{\left( {{x^4} - 1} \right)}^{ - 19}}}} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &= \int {{x^3}\frac{{{{\left( {{x^4} - 1} \right)}^{ - 20}}}}{{4{x^3}}}d} \left( {{x^4} - 1} \right) \hfill \\ &= \frac{1}{4} \cdot \frac{1}{{\left( { - 19} \right)}} \cdot {\left( {{x^4} - 1} \right)^{ - 19}} + c \hfill \\ &= \boxed{ - \frac{1}{{76{{\left( {{x^4} - 1} \right)}^{ - 19}}}} + c} \hfill \\ \end{align} $
$\begin{align} &u = {x^4} - 1 \hfill \\ &\frac{{du}}{{dx}} = 4{x^3} \to dx = \frac{{du}}{{4{x^3}}} \hfill \\ \end{align}$
$\begin{align} &= \int {\frac{{{x^3}}}{{{u^{20}}}}} \frac{{du}}{{4{x^3}}} \hfill \\ &= \frac{1}{4}\int {{u^{ - 20}}\; + c} \hfill \\ &= \frac{1}{4} \cdot \frac{1}{{\left( { - 19} \right)}}{u^{ - 19}} + c \hfill \\ &= \boxed{ - \frac{1}{{76{{\left( {{x^4} - 1} \right)}^{ - 19}}}} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &= \int {{x^3}\frac{{{{\left( {{x^4} - 1} \right)}^{ - 20}}}}{{4{x^3}}}d} \left( {{x^4} - 1} \right) \hfill \\ &= \frac{1}{4} \cdot \frac{1}{{\left( { - 19} \right)}} \cdot {\left( {{x^4} - 1} \right)^{ - 19}} + c \hfill \\ &= \boxed{ - \frac{1}{{76{{\left( {{x^4} - 1} \right)}^{ - 19}}}} + c} \hfill \\ \end{align} $
Soal 5
Pembahasan:
$\begin{align} &u = 2{x^3} - 8x + 3 \hfill \\ &\frac{{du}}{{dx}} = 6{x^2} - 8 \to dx = \frac{{du}}{{6{x^2} - 8}} \hfill \\ &= \int {\left( {3{x^2} - 4} \right){u^{ - \frac{1}{4}}}} \frac{{du}}{{2\left( {3{x^2} - 4} \right)}} \hfill \\ &= \frac{1}{2}\int {{u^{ - \frac{1}{4}}}\;} du \hfill \\ &= \frac{1}{2} \cdot \frac{4}{3}{u^{\frac{3}{4}}} + c \hfill \\ &= \boxed{\frac{2}{3}\sqrt[4]{{{{\left( {2{x^3} - 8x + 3} \right)}^3}}} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &= \int {\left( {3{x^2} - 4} \right)\frac{{{{\left( {2{x^3} - 8x + 3} \right)}^{ - \frac{1}{4}}}}}{{\left( {6{x^2} - 8} \right)}}} \;d\left( {2{x^3} - 8x + 3} \right) \hfill \\ &= \frac{1}{2} \cdot \frac{4}{3}{\left( {2{x^3} - 8x + 3} \right)^{\frac{3}{4}}} + c \hfill \\ &= \boxed{\frac{2}{3}\sqrt[4]{{{{\left( {2{x^3} - 8x + 3} \right)}^3}}} + c} \hfill \\ \end{align} $
$\begin{align} &u = 2{x^3} - 8x + 3 \hfill \\ &\frac{{du}}{{dx}} = 6{x^2} - 8 \to dx = \frac{{du}}{{6{x^2} - 8}} \hfill \\ &= \int {\left( {3{x^2} - 4} \right){u^{ - \frac{1}{4}}}} \frac{{du}}{{2\left( {3{x^2} - 4} \right)}} \hfill \\ &= \frac{1}{2}\int {{u^{ - \frac{1}{4}}}\;} du \hfill \\ &= \frac{1}{2} \cdot \frac{4}{3}{u^{\frac{3}{4}}} + c \hfill \\ &= \boxed{\frac{2}{3}\sqrt[4]{{{{\left( {2{x^3} - 8x + 3} \right)}^3}}} + c} \hfill \\ \end{align}$
${\text{Dengan menggunakan rumus:}}$
$\begin{align} &= \int {\left( {3{x^2} - 4} \right)\frac{{{{\left( {2{x^3} - 8x + 3} \right)}^{ - \frac{1}{4}}}}}{{\left( {6{x^2} - 8} \right)}}} \;d\left( {2{x^3} - 8x + 3} \right) \hfill \\ &= \frac{1}{2} \cdot \frac{4}{3}{\left( {2{x^3} - 8x + 3} \right)^{\frac{3}{4}}} + c \hfill \\ &= \boxed{\frac{2}{3}\sqrt[4]{{{{\left( {2{x^3} - 8x + 3} \right)}^3}}} + c} \hfill \\ \end{align} $
Soal 6
Pembahasan:
$\begin{align} &u = {x^2} + 9 \hfill \\ &\frac{{du}}{{dx}} = 2x \to dx = \frac{{du}}{{2x}} \hfill \\ &= \int\limits_0^4 {3x \cdot {u^{\frac{1}{2}}}} \frac{{du}}{{2x}} \hfill \\ &= \left. {\frac{3}{2} \cdot \frac{2}{3}{u^{\frac{3}{2}}}} \right|_{x = 0}^{x = 4} \hfill \\ &= \left. {u\sqrt u } \right|_{x = 0}^{x = 4} \hfill \\ &= \left. {\left( {{x^2} + 9} \right)\sqrt {{x^2} + 9} } \right|_0^4 \hfill \\ &= \left( {\left( {{4^2} + 9} \right)\sqrt {{4^2} + 9} } \right) - \left( {\left( {{0^2} + 9} \right)\sqrt {{0^2} + 9} } \right) \hfill \\ &= 125 - 27 \hfill \\ &= \boxed{98} \hfill \\\\ &{\text{Cara 2}} \hfill \\ &\left. {u\sqrt u } \right|_{x = 0}^{x = 4}{\text{ ganti batas }}x{\text{ dengan batas }}u \hfill \\ &u = {x^2} + 9 \hfill \\ &{\text{untuk }}x{\text{ = 0}} \to u = {0^2} + 9 = 9 \hfill \\ &{\text{untuk }}x{\text{ = 4}} \to u = {4^2} + 9 = 25 \hfill \\ &{\text{Sehingga bentuknya menjadi}} \hfill \\ &{\text{ = }}\left. {u\sqrt u } \right|_9^{25} \hfill \\ &= \left( {25\sqrt {25} } \right) - \left( {9\sqrt 9 } \right) \hfill \\ &= 125 - 27 \hfill \\ &= \boxed{98} \hfill \\ \end{align} $
$\begin{align} &u = {x^2} + 9 \hfill \\ &\frac{{du}}{{dx}} = 2x \to dx = \frac{{du}}{{2x}} \hfill \\ &= \int\limits_0^4 {3x \cdot {u^{\frac{1}{2}}}} \frac{{du}}{{2x}} \hfill \\ &= \left. {\frac{3}{2} \cdot \frac{2}{3}{u^{\frac{3}{2}}}} \right|_{x = 0}^{x = 4} \hfill \\ &= \left. {u\sqrt u } \right|_{x = 0}^{x = 4} \hfill \\ &= \left. {\left( {{x^2} + 9} \right)\sqrt {{x^2} + 9} } \right|_0^4 \hfill \\ &= \left( {\left( {{4^2} + 9} \right)\sqrt {{4^2} + 9} } \right) - \left( {\left( {{0^2} + 9} \right)\sqrt {{0^2} + 9} } \right) \hfill \\ &= 125 - 27 \hfill \\ &= \boxed{98} \hfill \\\\ &{\text{Cara 2}} \hfill \\ &\left. {u\sqrt u } \right|_{x = 0}^{x = 4}{\text{ ganti batas }}x{\text{ dengan batas }}u \hfill \\ &u = {x^2} + 9 \hfill \\ &{\text{untuk }}x{\text{ = 0}} \to u = {0^2} + 9 = 9 \hfill \\ &{\text{untuk }}x{\text{ = 4}} \to u = {4^2} + 9 = 25 \hfill \\ &{\text{Sehingga bentuknya menjadi}} \hfill \\ &{\text{ = }}\left. {u\sqrt u } \right|_9^{25} \hfill \\ &= \left( {25\sqrt {25} } \right) - \left( {9\sqrt 9 } \right) \hfill \\ &= 125 - 27 \hfill \\ &= \boxed{98} \hfill \\ \end{align} $
Soal 7
Pembahasan:
$\begin{align} &u = x + 3 \hfill \\ &\frac{{du}}{{dx}} = 1 \to dx = du \hfill \\ &= \int {2x \cdot {u^{\frac{1}{2}}}\;du} \hfill \\ \end{align} $
Perhatikan bentuk di atas masih mengandung $x$, sehingga kita perlu memanipulasi bentuk $x$ menjadi $u$.
$\begin{align} &u = x + 3 \to x = u - 3 \hfill \\ &= \int {2\left( {u - 3} \right)} \cdot {u^{\frac{1}{2}}}\;du \hfill \\ &= 2\int {{u^{\frac{3}{2}}} - 3{u^{^{\frac{1}{2}}}}} \;du \hfill \\ &= 2\left( {\frac{2}{5}{u^{\frac{5}{2}}} - 3 \cdot \frac{2}{3}{u^{\frac{3}{2}}}} \right) + c \hfill \\ &= 4{u^{\frac{3}{2}}}\left( {\frac{1}{5}u - 1} \right)\; + c\;\;\quad \left\{ {2{u^{\frac{3}{2}}}{\text{ dikeluarkan}}} \right\} \hfill \\ &= \frac{4}{5}u\sqrt u \left( {u - 5} \right) + c\;\;\quad \left\{ {{\text{samakan penyebut}}} \right\} \hfill \\ &= \boxed{\frac{4}{5}\left( {x - 2} \right)\left( {x + 3} \right)\sqrt {\left( {x + 3} \right)} + c} \hfill \\\\ &{\text{Cara alternatif}} \hfill \\ &\int {2x\sqrt {x + 3} } \;dx \hfill \\ &= 2\int {\left( {\left( {x + 3} \right) - 3} \right)\sqrt {x + 3} } \;dx \hfill \\ &= 2\left[ {\int {\left( {x + 3} \right)\sqrt {x + 3} } \;dx - 3\int {\sqrt {x + 3} } \;dx} \right] \hfill \\ &= 2\left[ {\int {{{\left( {x + 3} \right)}^{\frac{3}{2}}}dx - 3\int {{{\left( {x + 3} \right)}^{\frac{1}{2}}}} \;dx} } \right] \hfill \\ &= 2\left[ {\frac{2}{5}{{\left( {x + 3} \right)}^{\frac{5}{2}}} - 3 \cdot \frac{2}{3}{{\left( {x + 3} \right)}^{\frac{3}{2}}}} \right] + c \hfill \\ &= 4{\left( {x + 3} \right)^{\frac{3}{2}}}\left[ {\frac{{\left( {x + 3} \right)}}{5} - 1} \right] + c \hfill \\ &= \boxed{\frac{4}{5}\left( {x - 2} \right)\left( {x + 3} \right)\sqrt {\left( {x + 3} \right)} + c} \hfill \\ \end{align} $
$\begin{align} &u = x + 3 \hfill \\ &\frac{{du}}{{dx}} = 1 \to dx = du \hfill \\ &= \int {2x \cdot {u^{\frac{1}{2}}}\;du} \hfill \\ \end{align} $
Perhatikan bentuk di atas masih mengandung $x$, sehingga kita perlu memanipulasi bentuk $x$ menjadi $u$.
$\begin{align} &u = x + 3 \to x = u - 3 \hfill \\ &= \int {2\left( {u - 3} \right)} \cdot {u^{\frac{1}{2}}}\;du \hfill \\ &= 2\int {{u^{\frac{3}{2}}} - 3{u^{^{\frac{1}{2}}}}} \;du \hfill \\ &= 2\left( {\frac{2}{5}{u^{\frac{5}{2}}} - 3 \cdot \frac{2}{3}{u^{\frac{3}{2}}}} \right) + c \hfill \\ &= 4{u^{\frac{3}{2}}}\left( {\frac{1}{5}u - 1} \right)\; + c\;\;\quad \left\{ {2{u^{\frac{3}{2}}}{\text{ dikeluarkan}}} \right\} \hfill \\ &= \frac{4}{5}u\sqrt u \left( {u - 5} \right) + c\;\;\quad \left\{ {{\text{samakan penyebut}}} \right\} \hfill \\ &= \boxed{\frac{4}{5}\left( {x - 2} \right)\left( {x + 3} \right)\sqrt {\left( {x + 3} \right)} + c} \hfill \\\\ &{\text{Cara alternatif}} \hfill \\ &\int {2x\sqrt {x + 3} } \;dx \hfill \\ &= 2\int {\left( {\left( {x + 3} \right) - 3} \right)\sqrt {x + 3} } \;dx \hfill \\ &= 2\left[ {\int {\left( {x + 3} \right)\sqrt {x + 3} } \;dx - 3\int {\sqrt {x + 3} } \;dx} \right] \hfill \\ &= 2\left[ {\int {{{\left( {x + 3} \right)}^{\frac{3}{2}}}dx - 3\int {{{\left( {x + 3} \right)}^{\frac{1}{2}}}} \;dx} } \right] \hfill \\ &= 2\left[ {\frac{2}{5}{{\left( {x + 3} \right)}^{\frac{5}{2}}} - 3 \cdot \frac{2}{3}{{\left( {x + 3} \right)}^{\frac{3}{2}}}} \right] + c \hfill \\ &= 4{\left( {x + 3} \right)^{\frac{3}{2}}}\left[ {\frac{{\left( {x + 3} \right)}}{5} - 1} \right] + c \hfill \\ &= \boxed{\frac{4}{5}\left( {x - 2} \right)\left( {x + 3} \right)\sqrt {\left( {x + 3} \right)} + c} \hfill \\ \end{align} $
Soal 8
Pembahasan:
Jika kalian sudah memahami soal no 7 dengan baik maka dengan cara alternatif kita dapatkan bentuk:
$\begin{align} &= \int {\frac{{1 + x - 1}}{{\sqrt {1 + x} }}} \;dx \hfill \\ &= \int {\left( {1 + x} \right)} {\left( {1 + x} \right)^{ - \frac{1}{2}}}\;dx - \int {{{\left( {1 + x} \right)}^{ - \frac{1}{2}}}\;dx} \hfill \\ &= \int {{{\left( {1 + x} \right)}^{\frac{1}{2}}}\;dx} - \int {{{\left( {1 + x} \right)}^{ - \frac{1}{2}}}\;dx} \hfill \\ &= \frac{2}{3}{\left( {1 + x} \right)^{\frac{3}{2}}} - 2{\left( {1 + x} \right)^{\frac{1}{2}}} + c \hfill \\ &= 2{\left( {1 + x} \right)^{\frac{1}{2}}}\left( {\frac{{\left( {1 + x} \right)}}{3} - 1} \right) + c \hfill \\ &= \boxed{\frac{2}{3}\left( {x - 2} \right)\sqrt {1 + x} + c} \hfill \\ \end{align} $
Jika kalian sudah memahami soal no 7 dengan baik maka dengan cara alternatif kita dapatkan bentuk:
$\begin{align} &= \int {\frac{{1 + x - 1}}{{\sqrt {1 + x} }}} \;dx \hfill \\ &= \int {\left( {1 + x} \right)} {\left( {1 + x} \right)^{ - \frac{1}{2}}}\;dx - \int {{{\left( {1 + x} \right)}^{ - \frac{1}{2}}}\;dx} \hfill \\ &= \int {{{\left( {1 + x} \right)}^{\frac{1}{2}}}\;dx} - \int {{{\left( {1 + x} \right)}^{ - \frac{1}{2}}}\;dx} \hfill \\ &= \frac{2}{3}{\left( {1 + x} \right)^{\frac{3}{2}}} - 2{\left( {1 + x} \right)^{\frac{1}{2}}} + c \hfill \\ &= 2{\left( {1 + x} \right)^{\frac{1}{2}}}\left( {\frac{{\left( {1 + x} \right)}}{3} - 1} \right) + c \hfill \\ &= \boxed{\frac{2}{3}\left( {x - 2} \right)\sqrt {1 + x} + c} \hfill \\ \end{align} $
Soal 9
Pembahasan:
$\begin{align} &u = {x^2} - 1 \hfill \\ &\frac{{du}}{{dx}} = 2x \to dx = \frac{{du}}{{2x}} \hfill \\ &{\text{untuk }}x = 0 \to u = - 1{\text{ }} \hfill \\ &{\text{untuk }}x = 2 \to u = 3 \hfill \\ &{\text{Sehingga bentuknya menjadi:}} \hfill \\ &\int\limits_{ - 1}^3 {xf\left( u \right)\;\frac{{du}}{{2x}}} = 6 \hfill \\ &\frac{1}{2}\int\limits_{ - 1}^3 {f\left( u \right)\;du} = 6 \hfill \\ &\int\limits_{ - 1}^3 {f\left( u \right)\;du} = 12 \hfill \\ &\boxed{\int\limits_{ - 1}^3 {f\left( x \right)\;dx} = 12} \hfill \\ \end{align} $
$\begin{align} &u = {x^2} - 1 \hfill \\ &\frac{{du}}{{dx}} = 2x \to dx = \frac{{du}}{{2x}} \hfill \\ &{\text{untuk }}x = 0 \to u = - 1{\text{ }} \hfill \\ &{\text{untuk }}x = 2 \to u = 3 \hfill \\ &{\text{Sehingga bentuknya menjadi:}} \hfill \\ &\int\limits_{ - 1}^3 {xf\left( u \right)\;\frac{{du}}{{2x}}} = 6 \hfill \\ &\frac{1}{2}\int\limits_{ - 1}^3 {f\left( u \right)\;du} = 6 \hfill \\ &\int\limits_{ - 1}^3 {f\left( u \right)\;du} = 12 \hfill \\ &\boxed{\int\limits_{ - 1}^3 {f\left( x \right)\;dx} = 12} \hfill \\ \end{align} $
Soal 10
Pembahasan:
$\begin{align} &u = {x^3} + 2x \hfill \\ &\frac{{du}}{{dx}} = 3{x^2} + 2 \to dx = \frac{{du}}{{3{x^2} + 2}} \hfill \\ &= \int {\frac{{3{x^2} + 2}}{u}} \frac{{du}}{{3{x^2} + 2}} \hfill \\ &= \int {\frac{1}{u}\;du} \hfill \\ &= \ln \left| u \right| + c \hfill \\ &= \boxed{\ln \left| {{x^3} + 2x} \right| + c} \hfill \\ \end{align} $
$\begin{align} &u = {x^3} + 2x \hfill \\ &\frac{{du}}{{dx}} = 3{x^2} + 2 \to dx = \frac{{du}}{{3{x^2} + 2}} \hfill \\ &= \int {\frac{{3{x^2} + 2}}{u}} \frac{{du}}{{3{x^2} + 2}} \hfill \\ &= \int {\frac{1}{u}\;du} \hfill \\ &= \ln \left| u \right| + c \hfill \\ &= \boxed{\ln \left| {{x^3} + 2x} \right| + c} \hfill \\ \end{align} $


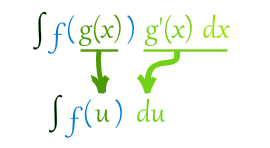


0 Komentar